LAmax calculation
One can be interested to come back to the LA,max value at the reference position (horizontal distance 7.5 m from the source and 1.2 m height) from the 1-hour equivalent sound level LA,eq[1hour] that is calculated from the DEUFRABASE.
Here, we present the methodology both for (2x1) lanes and (2x2) lanes, for a personal car at 90 km/h and 110 km/h (reference speed) and a heavy truck at 80 km/h (reference speed).
Personal car, 2x1 lanes, 90 km/h
Considering a personal car on a 2x1 lanes, and as shown before, there is a relation between the LA,max and LA,eq:
L_\text{A,max,DEUFRABASE}(V_\text{ref})=L_\text{A,eq,DEUFRABASE}[T](R_\text{ref})-10\log_{10}\left(\frac{\pi D_\text{ref}}{V_\text{ref}\times T}\right)
For a personal car at 90 km/h (reference speed), and for a reference position (d=7.5 m and h=1.20 m), for 1 hour, one have:
L_\text{A,max,DEUFRABASE}(V_\text{ref})=L_\text{A,eq,DEUFRABASE}[1 \text{hour}](R_\text{ref})+35.8\quad\text{dB(A)}
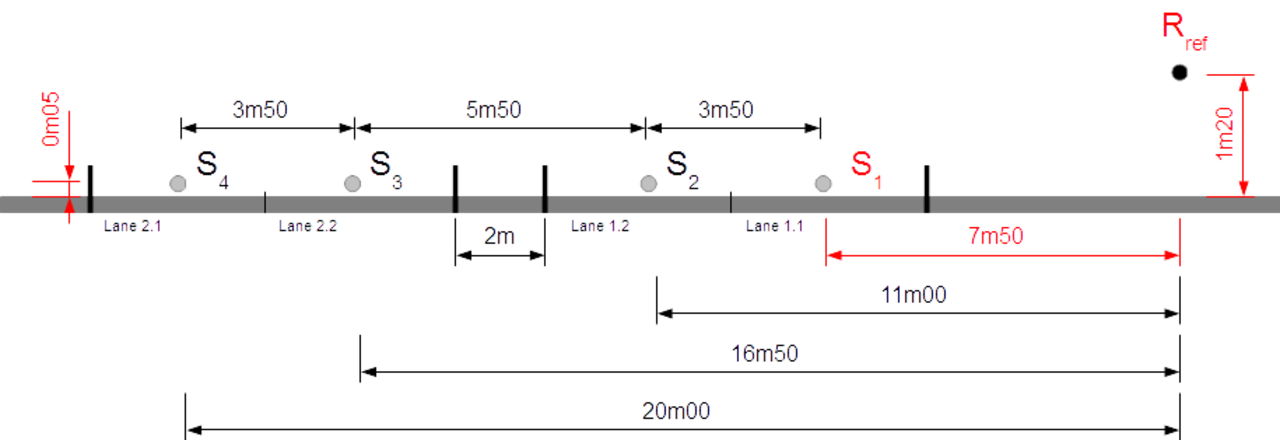
By default, the DEUFRABASE distributes all passenger cars (PC) equally on each direction, meaning that for a 2x1 lanes and for one PC per direction, you will have one PC on the first lane, i.e. the source S1, and 1 PC for the second lane, i.e; the source S2 (see details here).
By consequence, the total LA,max,DEUFRABASE is given by:
L_\text{A,max,DEUFRABASE}(V_\text{ref})=L_\text{A,max}\oplus\left[L_\text{A,max}+20\log\frac{D(S_1,R_\text{ref})}{D(S_2,R_\text{ref})}\right]
L_\text{A,max,DEUFRABASE}(V_\text{ref})=L_\text{A,max}\oplus\left(L_\text{A,max}-3.3\right)
L_\text{A,max}=L_\text{A,max,DEUFRABASE}(V_\text{ref})-1.7\quad\text{dB(A)}
Using the equation above for the LA,max,DEUFRABASE, with the last equation, the LA,max(1 hour) for a personal car can be obtained using this relation:
L_\text{A,max}=L_\text{A,eq,DEUFRABASE}\left[1 \text{hour}\right](R_\text{ref})+34.1\quad\text{dB(A)}
In practice, users have to carry out a simulation using a reference geometry (1a or 1b) with a corresponding pavement (Dense or Porous, respectively), then, to extract the LA,eq[1 hour] that are given by the DEUFRABASE and, lastly, to apply the last relation for each frequency band, in order to obtain the LA,max for each frequency band. Then, the global value is obtained by summing (in decibels) all frequency band contribution.
Personal car, 2x1 lanes, 110 km/h
Similarly, one can obtain LA,max value for a personal car, for a speed of 110 km/h, at the reference position (7.5 m from the source and 1.2 m height) on a 2x1 lanes, from the 1-hour equivalent sound level LA,eq[1h] that is calculated from the DEUFRABASE:
L_\text{A,max}=L_\text{A,eq,DEUFRABASE}\left[1 \text{hour}\right](R_\text{ref})+34.9\quad\text{dB(A)}
Heavy truck, 2x1 lanes, 80 km/h
Similarly, one can obtain LA,max value for a heavy truck, at the reference position (7.5 m from the source and 1.2 m height) on a 2x1 lanes, from the 1-hour equivalent sound level LA,eq[1h] that is calculated from the DEUFRABASE:
L_\text{A,max}=L_\text{A,eq,DEUFRABASE}\left[1 \text{hour}\right](R_\text{ref})+33.6\quad\text{dB(A)}