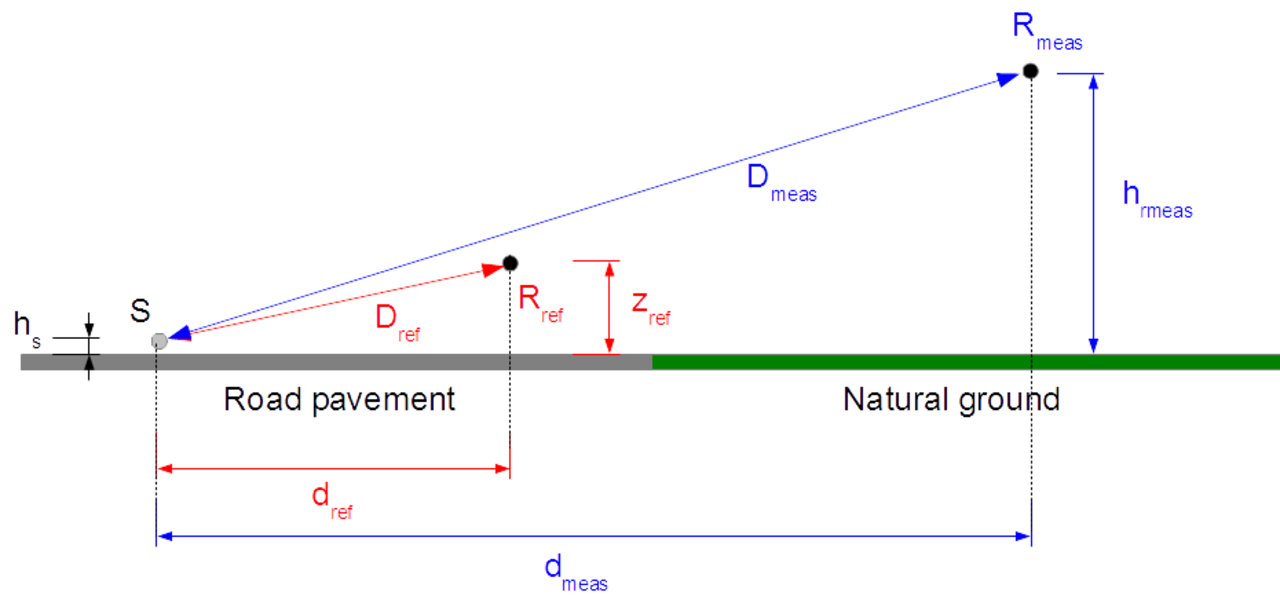
Equivalent sound level at a reference receiver Rref
From the measured LA,max, the equivalent sound level LA,eq[T] for the reference period T can be obtained from the general equation [BÉRENGIER, 1999]:
From the measured LA,max, the equivalent sound level LA,eq[T] for the reference period T can be obtained from the general equation [BÉRENGIER, 1999]:
where Dref is the distance between source and the reference microphone Rref, T the reference period which is taken equal to 1 hour and Vref the mean speed of the flow which depends on the situation (urban or suburban).
In a second step, the equivalent sound level at the receiver Rmeas at a distance Dmeas from the source is then calculated by the following relation:
Depending on the complexity of the road configuration, from geometrical and micro-meteorological points of view, several approaches have been used to pre-calculate this [Attenuation] term [BÉRENGIER, 2003; BÉRENGIER, 2007]:
For simple cases (flat dense/porous ground with/without impedance discontinuity, with/without positif sound celerity profile, i.e. geometry cases '1a' to '1d' of the DEUFRABASE) analytical models based on the ray tracing theory have been used. With those models, heterogeneous grounds and noise barriers [RASMUSSEN, 1982] with simple atmospheric effects (homogeneous and favorable conditions) can be easily investigated.
For more complex situations (up-slope/down-slope road, with/without impedance discontinuity, road with noise screen, i.e. geometry cases '2' to '4' of the DEUFRABASE) numerical approaches have been used:
Finally, this attenuation term can be expressed by the following relation:
The two first [Attenuation] terms concerns the attenuation due to propagation, calculated using the last procedures (due to the convention, these attenuation terms are considered as positive values). Since these attenuation are calculated relatively to the free field, they require to be corrected by the free field field propagation (third term). Lastly, the two last terms are due to the atmospheric attenuation (temperature T=20°C, relative humidity H=60%).
With the knowledge of the LA,eq[T=1 hour] for one vehicle representative of each vehicle family, i.e. personal car (PC) and heavy trucks (HT), the LA,eq[T] at a given receiver for a typical traffic flow on the various day (d) [6:00-18:00], evening (e) [18:00-22:00] and night (n) [22:00-6:00] periods (equivalent sound levels respectively noted Ld, Le and Ln), can be obtained by summing the respective energies of each vehicle as follow:
where nPC and nHT are, respectively, the number of passenger cars and heavy trucks in the traffic flow during the period T. LA,eq,PC and LA,eq,HT are the equivalent sound level at the receiver located in the far field, for one representative vehicle of each family on the reference period of 1 hour.
Afterwards, the common European noise indicator Lden (day-evening-night noise indicator, see the European directive 2002/49/EC) is obtained by summing all noise contributions on each period of the day (Ld), evening (Le) and night (Ln), including the weight of +5 dB for the evening and +10 dB for the night:
For sake of simplification, the calculation of the attenuation between the reference receiver [d(S,Rref) = 7.50 m and href = 1.20 m] and the measurement receiver [d(S,Rmeas) and hmeas] in the far field, are always carried out with respect to the median axis of the right traffic lane.
As the traffic is distributed among the different lanes (two or four depending on the road configuration), a set of excess attenuation relative to free field and geometrical attenuation should have been estimated for all the respective traffic lanes, that is not the case in the present version of the DEUFRABASE.
This assumption induces a small over-estimation of the resulting LA,eq or Lden. Moreover, considering the accuracy of the mean LA,max values for each pavement with respect to the measured LA,max distribution (± 3 dBA), the uncertainties on the LA,eq and Lden estimations are inside the LA,max range of variation.
Thus, this small over-estimation is acceptable and can be credited to the local residents, which consequently will be more protected when better effective means of traffic noise reduction will be installed (noise barriers, more efficient low noise pavements…).
When the receiver is very close to a reflecting façade, the reflection effect (+3 dB) has to be introduced accordingly at the very end of the procedure (the results produced by the DEUFRABASE does not take into account this reflection effect. Users have to add this +3 dB by hand in the results).
This procedure has been validated by comparison between theoretical results and several experiments for a large number of pavement families [BÉRENGIER, 2010]. The agreement was always within ±2 dB(A) at 200 m both for spectral and global LA,eq.
PREVIOUS: Principle
NEXT: Input parameters
References: